Mathematics
How to work out different probabilities in roulette
In this article I'm going to give you a simplified introduction to the mathematics of roulette.
I'm mostly going to be working out the probability of winning when betting on red (an even-money bet) on a European roulette table (the one with a single green 0), but you can use the same mathematics for working out the probabilities of winning with any bet on any table.
Probability
1. What's the probability of winning on one spin?

If you want to work out the probability of winning when betting on the red numbers, you can use a simple fraction like this:
18/37 = 0.48648In other words, there are a total of 37 numbers on the roulette wheel, and 18 of them are red, so we will win 18/37 times. If we put this fraction in to a calculator we get 0.48648, which is roughly 48.7%.
To work out the probability of other bets you do the same thing: put the total number of winning results over the total number of possible results:
Single Number: 1/37
Two Numbers: 2/37
Three Numbers: 3/37
Six Numbers: 6/37
Dozen: 12/37
Column: 12/37
Red: 18/37
Black: 18/37
Even: 18/37
Odd: 18/37
And that's all there is to working out basic probabilities. Just create a fraction that includes the number of times you can win over the total number of possibilities. This gives you the probability of winning, or "p" for short.
2. What's the probability of winning on multiple spins?
We can take this further by calculating the probability of winning multiple times in a row. We do this by multiplying individual probabilities together:
18/37 * 18/37 = 0.2366In other words, this tells us the probability of winning two times in a row when betting on red. The probability of winning on each individual spin is 18/37, and by multiplying them together we combine them to find the probability of winning over multiple spins.
Whenever you use the word "and" when working with probabilities, you're looking to multiply those things together.
We can work out the probability across further spins by multiplying even more probabilities together:
18/37 * 18/37 * 18/37 * 18/37 * 18/37 = 0.027249As you can see, the more times we try and win in a row, the lower the probability gets. That's what happens when you multiply fractions together.
Anyway, we can make the above easier to write down with the following mathematical notation:
(18/37)^5 = 0.027249This is the same thing as saying "18/37 multiplied by itself 5 times".
It's just easier to write it this way, rather than writing out the same fraction over and over again. So the next time you see it, you'll know it's shorthand for "the probability p of the same event happening over multiple spins x".
3. What's the probability of winning on any spin?
Instead of working out the probability of winning on one spin and another, we can also work out the probability of winning on one spin or another (notice the difference).
We do this by adding individual probabilities together:
18/37 + 18/37 = 0.97297So in other words, we have a 97.3% chance of winning at least once when betting on red over the course of two spins. We don't care to win both, we just want to know the probability of winning on one spin or the other.
Whenever you use the word "or" when working with probabilities, you're looking to add those things together.
This is interesting, but I'm only going to be multiplying probabilities throughout the rest of this article.
4. What's the probability of winning and losing in a specific order?

(I'm using green and red to represent winning and losing.)
We can use the same mathematics as above to help us to work out the probability of an exact series of results.
For example, we can work out the probability of winning the first two spins and then losing the next three spins:
18/37 * 18/37 * 19/37 * 19/37 * 19/37 = 0.032047If 18/37 numbers will win, then 19/37 (the rest of the numbers) will lose.
So there's a 3.2% chance of this exact sequence of results taking place over the course of the next five spins of the wheel. This was easy to work out, because we're just multiplying individual probabilities like we did before.
To simplify it we could write it like this:
(18/37)^2 * (19/37)^3 = 0.032047Again, this just shows the probability of winning two times and the probability of losing three times (in a specific order). Don't be put off by the mathematical notation, we're just using it to give us a quick way of writing down a specific scenario.
So over n spins we can work out the probability of winning x times and losing the rest of the time. For convenience we call the probability of losing "q".
5. What's the probability of winning and losing in any order?

But what if we don't care about the order? What if we want to know the probability of winning any two out of the next five spins? That's much more interesting.
To work this out, we first of all need to figure out all the possible combinations of ways we could win the next two out of five spins:
W W L L L
W L W L L
W L L W L
W L L L W
L W W L L
L W L W L
L W L L W
L L W W L
L L W L W
L L L W W
Combinations = 10
So we can see there are 10 combinations of ways we could win two out of five spins.
Therefore, to work out the probability of winning two out of five spins in any order, all we have to do now is add up all the individual probabilities of each of these sequences:
(18/37)^2 * (19/37)^3 = 0.032047
(18/37)^2 * (19/37)^3 = 0.032047
(18/37)^2 * (19/37)^3 = 0.032047
(18/37)^2 * (19/37)^3 = 0.032047
(18/37)^2 * (19/37)^3 = 0.032047
(18/37)^2 * (19/37)^3 = 0.032047
(18/37)^2 * (19/37)^3 = 0.032047
(18/37)^2 * (19/37)^3 = 0.032047
(18/37)^2 * (19/37)^3 = 0.032047
(18/37)^2 * (19/37)^3 = 0.032047
Total = 0.32047
So now we know there is a 32.1% chance of winning two out of any of the next five spins. All we needed to do was to work out the probability of winning two out of five spins in an exact order, then find out all the possible combinations of doing this, and add that many of those probabilities together.
To simplify the above mathematics, we could have just written something like this instead:
combinations * [(18/37)^2 * (19/37)^3] = 0.32047And like I say, for working out the probability of results in any order, you just need to be able to work out all the possible combinations to help you find the answer.
Combinations
Writing down all the combinations of winning two out of five spins was easy enough. But what if you wanted to know the combinations of winning two out of the next hundred spins? That's a lot of combinations to write down.
Fortunately there is a formula we can use to easily work out the number of combinations of something:
n = number of spins
x = number of wins
combinations = n!/[x!(n-x)!]
For example, this formula gives us all the arrangements of ways in which we could win 2 out of the next 5 spins:
5 = number of spins
2 = number of wins
combinations = 5! / [2! * 3!]
= 5*4*3*2*1 / [ (2*1) * (3*2*1) ]
= 5*4 / 2*1
= 20 / 2
= 10
It also works for much larger combinations like winning 2 out of 100 spins:
100 = number of spins
2 = number of wins
combinations = 100! / [2! * 98!]
= 100*99 / 2*1
= 9900 / 2
= 4950
Very handy.
Don't be put off by the formula: it's just a tool to work out the number of possible combinations when choosing x things from n elements.
I'm not going to explain where this formula comes from because I want to carry on with the mathematics in roulette. But if you're interested, here's an excellent page on working out permutations and combinations.
| Rank | Casino | Rating | Payment Methods | Payout Time | Links |
|---|---|---|---|---|---|
| 1 |
|
Rating A+ | Payment Methods | Payout Time 1-2 Days | Play Now Read Review |
| 2 |
|
Rating A | Payment Methods | Payout Time 1-2 Days | Play Now Read Review |
Binomial Distribution
Binomial: "Bi" means two and "nomial" means terms. The two "terms" we are looking at are the probability of winning and the probability of losing.
Now we can work out all the probabilities for winning 1, 2, 3, 4, 5, etc. out of 100 spins, and see how they all compare.
For example, we can work out the probability of winning 1 out of 100 spins like so:
(18/37)^1 * (19/37)^99But that's for winning once at a specific point over 100 spins. We want to work all the combinations of ways this could happen, because we we're happy for the win to come at any time:
combinations = 100! / [1! * 99!]
= 100
So there are 100 ways we could win 1 out of 100 spins (which makes sense when you think about it, because there are 100 different positions where the single win could take place).
But anyway, multiplying the probability of a specific sequence by all the possible combinations gives us:
combinations * probability of specific sequence = 100 * (18/37)^1 * (19/37)^99
= 0.0000000000000000000000000010757
So pretty slim odds.
Anyway, we can repeat this process to find the probabilities for winning x out of 100 spins. Here are all the results:
0/100: 1 * (18/37)^0 * (19/37)^100 = 0.0000000000000000000000000000113550143810
1/100: 100 * (18/37)^1 * (19/37)^99 = 0.0000000000000000000000000010757382045112
2/100: 4,950 * (18/37)^2 * (19/37)^98 = 0.0000000000000000000000000504464600115506
3/100: 161,700 * (18/37)^3 * (19/37)^97 = 0.0000000000000000000000015611851835153547
4/100: 3,921,225 * (18/37)^4 * (19/37)^96 = 0.0000000000000000000000358661754002343675
5/100: 75,287,520 * (18/37)^5 * (19/37)^95 = 0.0000000000000000000006523868535958416060
6/100: 1,192,052,400 * (18/37)^6 * (19/37)^94 = 0.0000000000000000000097858028039376300151
7/100: 16,007,560,800 * (18/37)^7 * (19/37)^93 = 0.0000000000000000001244930702576125543371
8/100: 186,087,894,300 * (18/37)^8 * (19/37)^92 = 0.0000000000000000013710618395476536614822
9/100: 1,902,231,808,400 * (18/37)^9 * (19/37)^91 = 0.0000000000000000132776514987772775638273
10/100: 17,310,309,456,440 * (18/37)^10 * (19/37)^90 = 0.0000000000000001144673323947221008585713
11/100: 141,629,804,643,600 * (18/37)^11 * (19/37)^89 = 0.0000000000000008872587487055007245768114
12/100: 1,050,421,051,106,700 * (18/37)^12 * (19/37)^88 = 0.0000000000000062341601553781281363361920
13/100: 7,110,542,499,799,204 * (18/37)^13 * (19/37)^87 = 0.0000000000000399793914417771580110803253
14/100: 44,186,942,677,323,584 * (18/37)^14 * (19/37)^86 = 0.0000000000002353673947286577550385257133
15/100: 253,338,471,349,988,800 * (18/37)^15 * (19/37)^85 = 0.0000000000012784165861051319249087778617
16/100: 1,345,860,629,046,814,720 * (18/37)^16 * (19/37)^84 = 0.0000000000064341361077001674301982449038
17/100: 6,650,134,872,937,201,664 * (18/37)^17 * (19/37)^83 = 0.0000000000301189281574075947653972338873
18/100: 30,664,510,802,988,204,032 * (18/37)^18 * (19/37)^82 = 0.0000000001315721598455174005840639349645
19/100: 132,341,572,939,212,275,712 * (18/37)^19 * (19/37)^81 = 0.0000000005379515455179604866610794696835
20/100: 535,983,370,403,809,853,440 * (18/37)^20 * (19/37)^80 = 0.0000000020640351404347021271369446625494
21/100: 2,041,841,411,062,131,589,120 * (18/37)^21 * (19/37)^79 = 0.0000000074491493790124540841778083479375
22/100: 7,332,066,885,177,660,407,808 * (18/37)^22 * (19/37)^78 = 0.0000000253413646338653587554482187870625
23/100: 24,865,270,306,254,660,567,040 * (18/37)^23 * (19/37)^77 = 0.0000000814171074277962248192248547254413
24/100: 79,776,075,565,900,366,872,576 * (18/37)^24 * (19/37)^76 = 0.0000002474651554713279688206594222887880
25/100: 242,519,269,720,337,158,242,304 * (18/37)^25 * (19/37)^75 = 0.0000007126996477574248678408543565543365
26/100: 699,574,816,500,972,471,189,504 * (18/37)^26 * (19/37)^74 = 0.0000019476609807136099248258114674525743
27/100: 1,917,353,200,780,442,800,750,592 * (18/37)^27 * (19/37)^73 = 0.0000050570846516774439822930302390613377
28/100: 4,998,813,702,034,726,544,474,112 * (18/37)^28 * (19/37)^72 = 0.0000124906188577145929976316279796932918
29/100: 12,410,847,811,948,290,443,837,440 * (18/37)^29 * (19/37)^71 = 0.0000293790236653323393392622797648527921
30/100: 29,372,339,821,610,946,892,136,448 * (18/37)^30 * (19/37)^70 = 0.0000658708635864819791764721013116457016
31/100: 66,324,638,306,863,454,235,918,336 * (18/37)^31 * (19/37)^69 = 0.0001409122039371261741677598955391204072
32/100: 143,012,501,349,174,321,585,586,176 * (18/37)^32 * (19/37)^68 = 0.0002878502587005110765691617835670967906
33/100: 294,692,427,022,540,688,947,412,992 * (18/37)^33 * (19/37)^67 = 0.0005619277777502794781264161549927393935
34/100: 580,717,429,720,889,503,917,277,184 * (18/37)^34 * (19/37)^66 = 0.0010490478327660026410667049034941555874
35/100: 1,095,067,153,187,963,076,310,204,416 * (18/37)^35 * (19/37)^65 = 0.0018740884591368588401455452796540157578
36/100: 1,977,204,582,144,933,240,600,788,992 * (18/37)^36 * (19/37)^64 = 0.0032056776274709429183640274629851774080
37/100: 3,420,029,547,493,939,811,572,514,816 * (18/37)^37 * (19/37)^63 = 0.0052531161121572239949828464489200996468
38/100: 5,670,048,986,634,688,515,759,144,960 * (18/37)^38 * (19/37)^62 = 0.0082507391567677168531247389182681217790
39/100: 9,013,924,030,034,634,124,564,627,456 * (18/37)^39 * (19/37)^61 = 0.0124262144385327583800959772020178206731
40/100: 13,746,234,145,802,810,415,403,499,520 * (18/37)^40 * (19/37)^60 = 0.0179526098072486338386166693226186907850
41/100: 20,116,440,213,369,981,264,747,036,672 * (18/37)^41 * (19/37)^59 = 0.0248893691807811866245625509463934577070
42/100: 28,258,808,871,162,573,880,278,646,784 * (18/37)^42 * (19/37)^58 = 0.0331234462029944831673589078491204418242
43/100: 38,116,532,895,986,721,524,916,682,752 * (18/37)^43 * (19/37)^57 = 0.0423266558579268592499289525221684016287
44/100: 49,378,235,797,073,732,718,773,141,504 * (18/37)^44 * (19/37)^56 = 0.0519463503710920898592817707140056882054
45/100: 61,448,471,214,136,243,133,410,705,408 * (18/37)^45 * (19/37)^55 = 0.0612420130690770544990009227603877661750
46/100: 73,470,998,190,815,045,584,871,751,680 * (18/37)^46 * (19/37)^54 = 0.0693702436365975366738823026935278903693
47/100: 84,413,487,283,064,058,245,720,047,616 * (18/37)^47 * (19/37)^53 = 0.0755071408900031132427344005009217653424
48/100: 93,206,558,875,049,914,871,998,054,400 * (18/37)^48 * (19/37)^52 = 0.0789844434309901199942061111869406886399
49/100: 98,913,082,887,808,056,769,296,465,920 * (18/37)^49 * (19/37)^51 = 0.0794086348565056637793801996849651914090
50/100: 100,891,344,545,564,237,256,087,044,096 * (18/37)^50 * (19/37)^50 = 0.0767338176823918055591278175597835797817
51/100: 98,913,082,887,808,056,769,296,465,920 * (18/37)^51 * (19/37)^49 = 0.0712697997050078524416960590315284207463
52/100: 93,206,558,875,049,914,871,998,054,400 * (18/37)^52 * (19/37)^48 = 0.0636234446759280786176660171804542187601
53/100: 84,413,487,283,064,058,245,720,047,616 * (18/37)^53 * (19/37)^47 = 0.0545885364448876406195942934118647826836
54/100: 73,470,998,190,815,045,584,871,751,680 * (18/37)^54 * (19/37)^46 = 0.0450116002264863285242668666796816978604
55/100: 61,448,471,214,136,243,133,410,705,408 * (18/37)^55 * (19/37)^45 = 0.0356646937679719611136164303388795815408
56/100: 49,378,235,797,073,732,718,773,141,504 * (18/37)^56 * (19/37)^44 = 0.0271507537143395455414562889018270652741
57/100: 38,116,532,895,986,721,524,916,682,752 * (18/37)^57 * (19/37)^43 = 0.0198553988381873561253065929577132919803
58/100: 28,258,808,871,162,573,880,278,646,784 * (18/37)^58 * (19/37)^42 = 0.0139456249553148985825812289363057061564
59/100: 20,116,440,213,369,981,264,747,036,672 * (18/37)^59 * (19/37)^41 = 0.0094048996130402066906395219803016516380
60/100: 13,746,234,145,802,810,415,403,499,520 * (18/37)^60 * (19/37)^40 = 0.0060884350126523406609990729521086905152
61/100: 9,013,924,030,034,634,124,564,627,456 * (18/37)^61 * (19/37)^39 = 0.0037822892227003346125868699090233349125
62/100: 5,670,048,986,634,688,515,759,144,960 * (18/37)^62 * (19/37)^38 = 0.0022539618288078388380624161868581722956
63/100: 3,420,029,547,493,939,811,572,514,816 * (18/37)^63 * (19/37)^37 = 0.0012879781878901942412940506699214893160
64/100: 1,977,204,582,144,933,240,600,788,992 * (18/37)^64 * (19/37)^36 = 0.0007054222640911752889233965468918086117
65/100: 1,095,067,153,187,963,076,310,204,416 * (18/37)^65 * (19/37)^35 = 0.0003701324916041147427073210174341966194
66/100: 580,717,429,720,889,503,917,277,184 * (18/37)^66 * (19/37)^34 = 0.0001859517302317322689792639112127403678
67/100: 294,692,427,022,540,688,947,412,992 * (18/37)^67 * (19/37)^33 = 0.0000893970611954595999974065856363836247
68/100: 143,012,501,349,174,321,585,586,176 * (18/37)^68 * (19/37)^32 = 0.0000411005064629280699849828151215547223
69/100: 66,324,638,306,863,454,235,918,336 * (18/37)^69 * (19/37)^31 = 0.0000180578884230713739348066909640166955
70/100: 29,372,339,821,610,946,892,136,448 * (18/37)^70 * (19/37)^30 = 0.0000075761667218600199424699201400379422
71/100: 12,410,847,811,948,290,443,837,440 * (18/37)^71 * (19/37)^29 = 0.0000030327131429239518159749703501981699
72/100: 4,998,813,702,034,726,544,474,112 * (18/37)^72 * (19/37)^28 = 0.0000011572194887472972307139928646591009
73/100: 1,917,353,200,780,442,800,750,592 * (18/37)^73 * (19/37)^27 = 0.0000004205036930992342402354784540452481
74/100: 699,574,816,500,972,471,189,504 * (18/37)^74 * (19/37)^26 = 0.0000001453519166758377450217803528512150
75/100: 242,519,269,720,337,158,242,304 * (18/37)^75 * (19/37)^25 = 0.0000000477366294766962031617290641589274
76/100: 79,776,075,565,900,366,872,576 * (18/37)^76 * (19/37)^24 = 0.0000000148763734518790080226177538957541
77/100: 24,865,270,306,254,660,567,040 * (18/37)^77 * (19/37)^23 = 0.0000000043927500555104123048687460230833
78/100: 7,332,066,885,177,660,407,808 * (18/37)^78 * (19/37)^22 = 0.0000000012271245094340833790272521656908
79/100: 2,041,841,411,062,131,589,120 * (18/37)^79 * (19/37)^21 = 0.0000000003237450404636220408695121352832
80/100: 535,983,370,403,809,853,440 * (18/37)^80 * (19/37)^20 = 0.0000000000805102797995060714072368325978
81/100: 132,341,572,939,212,275,712 * (18/37)^81 * (19/37)^19 = 0.0000000000188328139881885493865399402834
82/100: 30,664,510,802,988,204,032 * (18/37)^82 * (19/37)^18 = 0.0000000000041340323388706573006248991275
83/100: 6,650,134,872,937,201,664 * (18/37)^83 * (19/37)^17 = 0.0000000000008493509687977762079950409815
84/100: 1,345,860,629,046,814,720 * (18/37)^84 * (19/37)^16 = 0.0000000000001628454864988217921246867552
85/100: 253,338,471,349,988,800 * (18/37)^85 * (19/37)^15 = 0.0000000000000290399381496351189330936285
86/100: 44,186,942,677,323,584 * (18/37)^86 * (19/37)^14 = 0.0000000000000047985209916777686422425991
87/100: 7,110,542,499,799,204 * (18/37)^87 * (19/37)^13 = 0.0000000000000007315349606187531791205460
88/100: 1,050,421,051,106,700 * (18/37)^88 * (19/37)^12 = 0.0000000000000001023798928138685688215618
89/100: 141,629,804,643,600 * (18/37)^89 * (19/37)^11 = 0.0000000000000000130775025711387363655193
90/100: 17,310,309,456,440 * (18/37)^90 * (19/37)^10 = 0.0000000000000000015142371398160656055231
91/100: 1,902,231,808,400 * (18/37)^91 * (19/37)^9 = 0.0000000000000000001576418074996481270019
92/100: 186,087,894,300 * (18/37)^92 * (19/37)^8 = 0.0000000000000000000146098242648415368608
93/100: 16,007,560,800 * (18/37)^93 * (19/37)^7 = 0.0000000000000000000011906138619904821379
94/100: 1,192,052,400 * (18/37)^94 * (19/37)^6 = 0.0000000000000000000000839962746980967443
95/100: 75,287,520 * (18/37)^95 * (19/37)^5 = 0.0000000000000000000000050258158822129894
96/100: 3,921,225 * (18/37)^96 * (19/37)^4 = 0.0000000000000000000000002479843362934042
97/100: 161,700 * (18/37)^97 * (19/37)^3 = 0.0000000000000000000000000096879393451574
98/100: 4,950 * (18/37)^98 * (19/37)^2 = 0.0000000000000000000000000002809606469595
99/100: 100 * (18/37)^99 * (19/37)^1 = 0.0000000000000000000000000000053772372624
100/100: 1 * (18/37)^100 * (19/37)^0 = 0.0000000000000000000000000000000509422477
Note: All of these individual values add up to 1.
If we put all these results in a chart, we get this:
Note: Some of the numbers are too small to show up on the chart, but they are there.
And there we have it. Now we can see all the probabilities of winning x out of the next 100 spins of the roulette wheel when betting on red (where each of those x wins could come in any particular order). It took a bit of mathematics, but we got there in the end.
For what it's worth, this is called a binomial distribution. The formula for this is:
Which is just a mathematical formula for working out what we have just done.
Mathematics is full of equations that describe basic logic. They only ever seem complex because you've got to work backwards to figure out the actual method that it's describing.
Mathematical formulas are never explanations on there own. They're just condensed representations of logic. It takes some time (and experience) to get the hang of breaking them down and figure out what they're trying to say. So don't be afraid of equations; I don't know anyone who sees a new equation and gets it at first glance.
Code
# -----------------------------
# Binomial Distribution Formula
# -----------------------------
# Allows you to work out the probability of x successes over n trials.
#
# P(x) = n!/[x! * (n-x)!] * p^x * q^(n-x)
#
# n = number of trials
# x = number of successful trials
# p = probability of success
# q = probability of failure
#
# Criteria:
# * Each trial is independent.
# * There are only two possible outcomes from each trial.
# * The probability of success and failure stays the same.
# Factorial function
def factorial(n)
# create a range from 1 to n and multiply together (return 1 if n is zero)
(1..n).inject(:*) || 1
end
# Variables
n = 100 # number of spins
p = 18/37r # probability of winning (18 red numbers out of 37 on the wheel)
q = 1 - p # probability of losing (all the remaining numbers)
# Work out binomial probability for each x number of wins out of 100 (e.g. 0/100, 1/100, 2/100, etc.)
0.upto(n) do |x|
# Combinations of ways we can win that number of times
combinations = factorial(n) / (factorial(x) * factorial(n - x))
# Probability of winning x out of n times (in one specific order)
probability = p ** x * q ** (n - x)
# Multiply together
result = combinations * probability
# Print results (converting from rational number and showing 40 decimal places)
puts "#{x} #{"%.40f" % result.to_f}"
endStatistics
Now that we've got our probability distribution for winning at roulette, we can use a handful of handy formulas to find out more interesting statistics about it.
Before we get started I just want to make a note of these three variables:
n = 100 <- number of spins
p = 18/37 <- probability of winning
q = 19/37 <- probability of losing (same as 1-p)
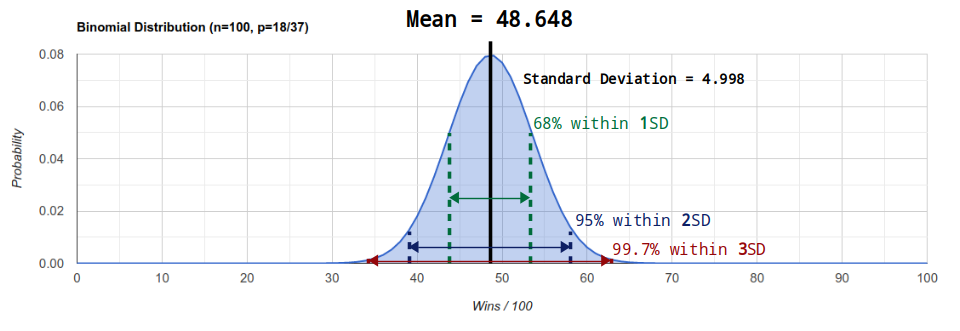
1. Mean
mean = n*p
= 100*(18/37)
= 48.648
The mean tells us the average number of times we can expect to win over a number of spins.
So in our example over 100 spins with a probability of winning 18/37 on each spin, we can expect to win an average of 48.648 times.
2. Variance
variance = n*p*q
= 100*(18/37)*(19/37)
= 24.981
The variance indicates how spread out each of the probabilities are from the average.
This number doesn't tell us much on it's own, because it's not in the same units as "number of wins". So it's not like we're saying "ah yes, 24.981, of course!" Instead, this number is only really useful for comparing the shapes of different probability distributions:
So we can see that the probabilities are most spread out when betting on red/black, and least spread out when betting on single number. In other words, you're more likely to see a range of different results when betting on red/black (i.e. in the range of 40-60 wins out of 100), whereas your results are more concentrated around a fixed point when betting on a single number (i.e. in the range of 1-5 wins out of 100).
The peak of each distribution also helps you to identify the most common number of times you expect to win over 100 spins for each bet.
However, whilst the variance is only useful for describing the spread of results and the shape of the distribution, it's actually a stepping stone toward getting a more useful number in the form of the standard deviation...
3. Standard Deviation
standard deviation = sqrt(n*p*q)
= sqrt(100*(18/37)*(19/37))
= sqrt(24.981)
= 4.998
The standard deviation (SD) tells us what the "typical" deviation is from the mean. It's similar to variance, but this time the actual number is relevant (because the units are back in number of wins).
For example, when betting on red, the mean tells us that can we expect to win an average of 48.648 times out of a 100, and the standard deviation tells us that we should expect to be within 4.998 wins either side of this on a "typical" run.
Furthermore, there are some useful facts about this standard deviation:
- 68% of the time we expect to be within 1 SD (
±4.998) - 95% of the time we expect to be within 2 SD (
±9.996) - 99.7% of the time we expect to be within 3 SD (
±14.994)
| Bet (numbers covered) | Mean | SD |
|---|---|---|
| Even Money (18/37) | 48.648 | 4.998 |
| Column/Dozen (12/37) | 32.432 | 4.681 |
| Double Street (6/37) | 16.216 | 3.685 |
| Corner Bet (4/37) | 10.810 | 3.105 |
| Street Bet (3/37) | 8.108 | 2.729 |
| Split Bet (2/37) | 5.405 | 2.261 |
| Single Number (1/37) | 2.702 | 1.621 |
So basically, the standard deviation helps us to determine if our results over a certain number of spins is statistically "normal" or not.
Code
# --------------------------------
# Binomial Distribution Statistics
# --------------------------------
n = 100 # number of trials
p = 18/37r # probability of success (a bet on the red numbers)
q = 1 - p # probability of failure
# 1. Mean (the average expected number of wins)
mean = n * p
# 2. Variance (the spread of the results from the average)
variance = mean * q
# 3. Standard Deviation (the typical expected deviation from the average)
standard_deviation = Math.sqrt(variance)
# Show results
puts "n = #{n}"
puts "p = #{p}"
puts "q = #{q}"
puts
puts "Mean = #{mean.to_f}" # convert from fraction to decimal (from rational to float)
puts "Variance = #{variance.to_f}"
puts "Standard Deviation = #{standard_deviation}"Conclusion
The mathematics of roulette is just fractions and multiplication.
The mathematics of roulette isn't too difficult. It's essentially working out the individual probabilities of winning, and multiplying them together to work out overall probability of winning over multiple spins.
I'm hoping that the mathematics in this article was easy to follow. Mathematics can appear daunting at first, especially when you run in to terms like "binomial distribution" alongside complex-looking formulas, but when you peel back the terminology the logic is rarely as difficult as it seems.
Lastly, if you're going to take anything from this article, it should be the fact that you're going to win an average of 48.648 out of 100 spins when betting on red.
What does that mean? It means that you're mathematically expected to lose more times than you win. You can try all sorts of systems and place your bets in all kinds of ways, but this number never changes. It's what gives the casino the edge, and it's why you can never beat the game no matter how hard you try.
But on the other hand, at least working out the math was fun.
Links
- Binomial Distribution:
- The Binomial Distribution (mathsisfun.com)
- Binomial Formula Explained (mathnstuff.com)
- Combinations:
- Combinations and Permutations (mathsisfun.com)
- Statistics:
- Mean, Variance, and Standard Deviation of Binomial Distribution (David Arnold)
- Variance and Standard Deviation (mathbitsnotebook.com)