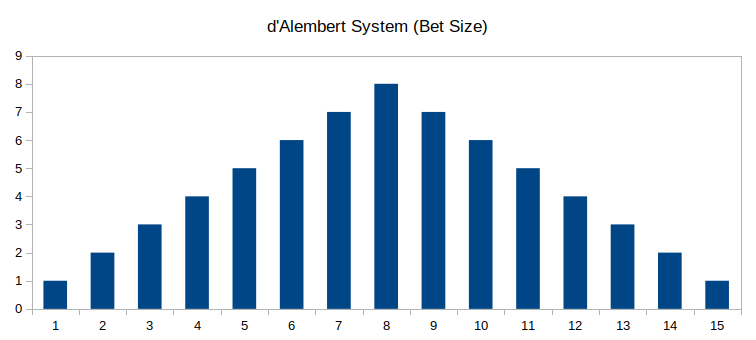
The d'Alembert System

• Also known as: Pyramid System, Seesaw System , Montant et démontant (Upwards and downwards)
• Type: Negative Progression

The d'Alembert system is a simple betting system where you increase or decrease the size of your bet by one unit each time you lose or win when betting on red/black (or any other even money bet) in roulette.

• If you lose, you increase your bet by one unit.
• If you win, you decrease your bet by one unit.

This means as you you go on a losing streak you gradually increase the size of your bet as you go. And as you begin to win again, your bet size gradually returns back to your original betting unit:

Losing the first 7 spins in a row and then winning the next 8.

As a result, the increased size of your bets after a losing streak means that you should be able recoup your losses with a fewer number of spins, and ideally return to winning money when the results of the wheel have "evened out".

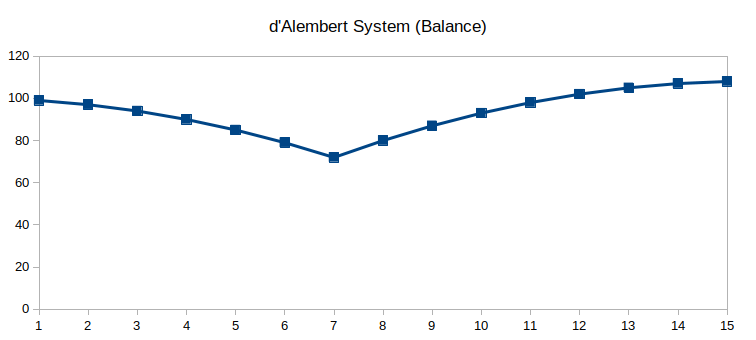
Losses are recuperated gradually using the d'Alembert system (as opposed to instantly like in the martingale system).

d'Alembert system simulation

This simulation shows the possible results of betting according to the d'Alembert system over a given number of spins of the roulette wheel.

The overall trend when using the d'Alembert is always downwards, even though it's sometimes punctuated by the occasional recuperative winning streak.

Algorithm / Code

# Settings
unit = 1
balance = 100
spins = 500

# Set the initial bet size
bet = unit

# Repeat for a given number of spins
spins.times do |i|

  # Spin the roulette wheel
  result = rand(0..36)

  # Check if the result is a win
  win = (result >= 19) # using the high numbers as the even-money wager

  # Print bet size and result
  print "Spin #{i}: bet=#{bet} #{win ? "(win)" : "(lose)"}, "

  if win
    # Update balance
    balance = balance + bet

    # Decrease the bet size by one unit (if we are above the initial unit size)
    if bet > unit
      bet = bet - unit
    end
  else
    # Update balance
    balance = balance - bet

    # Increase the bet size by one unit
    bet = bet + unit
  end

  # Print new balance
  print "balance=#{balance}\n"
end

What's the theory behind the d'Alembert system?

The system is founded on the theory that after a series of losing spins on the roulette wheel, the next spin is more likely to win.

For example, if you're betting on black and the wheel has come up red over the last ten spins, then the d'Alembert system operates on the belief that it's more likely that black is going to show up next.

The d'Alembert system tries to capitalize on this belief by increasing the size of your bet with every successive losing spin, so that you can win more when the results eventually "rebalance" back in to your favor.

Note: The system assumes that the roulette wheel wants to reach a level of equilibrium in the results.

Who invented the d'Alembert system?

The system is named after Jean le Rond d'Alembert, who was a French physicist and mathematician who lived between 1717-1783.

He didn't invent the betting system itself (roulette wasn't invented until after his death in 1796), but he did believe in the "equilibrium effect" when it came to the results of coin flips. He believed that if the result of a coin flip came up Heads, then it was more likely that Tails would be the result of the next flip.

The roulette system was devised later on and named in his honor.

Does the system work?

Not to win money, no.

Why is the system flawed?

Because the whole basis of the system if founded on what is known as the gambler's fallacy.

The gambler's fallacy in roulette is the false belief that the result of previous spins will affect the result of future spins.

For example, if the result has been red for the last 100 spins, the chance of the result of the next spin being red is still 50/50 (ignoring the possibility of the green number).

Why? Because the roulette wheel has no memory.

From our outside perspective we can see that red has come up every time for the last 100 spins, but that doesn't affect the behavior of the roulette wheel. We may "feel" that black should come up, but the roulette wheel doesn't care.

This is not how roulette wheels think.

In other words, every spin of the roulette wheel is independent of the last.

So in summary, the system has been designed using a principle that doesn't exist. Every bet you make is going to be subject to the house edge, and unfortunately there are no hidden forces in the universe that conspire to balance your results for you and make this system work.

If you've lost on the last few spins and decide to increase the size of your bet, you're not increasing your chances of winning money — you're just increasing your risk.

Conclusion

The d'Alembert system is founded on the age-old belief that your chance of winning increases with every successive loss.

But this just isn't how probability works.

If you play roulette for long enough you'll see crazier results than you ever thought possible. Just ask any croupier and I'm sure they'll have plenty of stories to tell you about the roulette wheel. But at the end of the day, you just have to accept that the next spin of the wheel is completely independent from any and every result you have ever seen before.

But what's most interesting of all is that the basics of probability can trip up even the greatest of minds.

Jean le Rond d'Alembert was a renowned mathematician, but for some reason even the laws of probability escaped his logical prowess. He could provide a solution to the one-dimensional wave equation, but he couldn't appreciate how the results of independent events do not have any influence on each other.

So if you've ever mistakenly thought the same thing, at least you're in good company.

If nothing else, the failure of the d'Alembert system provides a valuable introduction to the deceptive nature of probability.

You can use it if you want, but it's not going to help win you any money.