Probability
The probability of winning with each bet
Here are a bunch of charts and tables for different probabilities in both European and American roulette.
There's also some handy (but not necessarily easy) information at the bottom about working out roulette probabilities, plus a little bit on the gambler's fallacy.
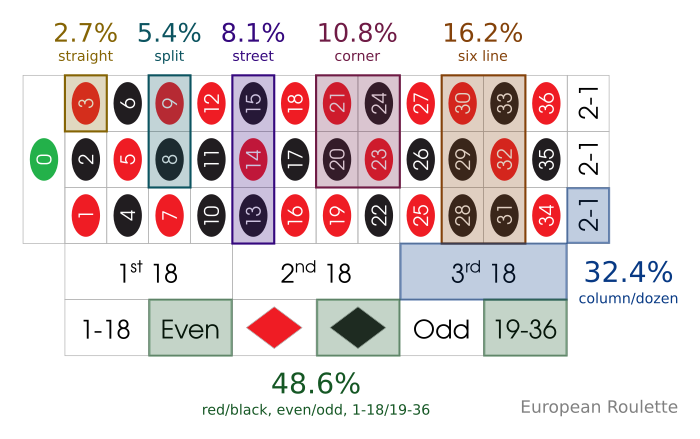
1. European roulette
| Bet Type | Fraction | Ratio | Percentage |
|---|---|---|---|
| Even (e.g. Red/Black) | 1/2.06 | 1.06 to 1 | 48.6% |
| Column | 1/3.08 | 2.08 to 1 | 32.4% |
| Dozen | 1/3.08 | 2.08 to 1 | 32.4% |
| Six Line | 1/6.17 | 5.17 to 1 | 16.2% |
| Corner | 1/9.25 | 8.25 to 1 | 10.8% |
| Street | 1/12.33 | 11.33 to 1 | 8.1% |
| Split | 1/19.50 | 18.50 to 1 | 5.4% |
| Straight | 1/37.00 | 36.00 to 1 | 2.7% |
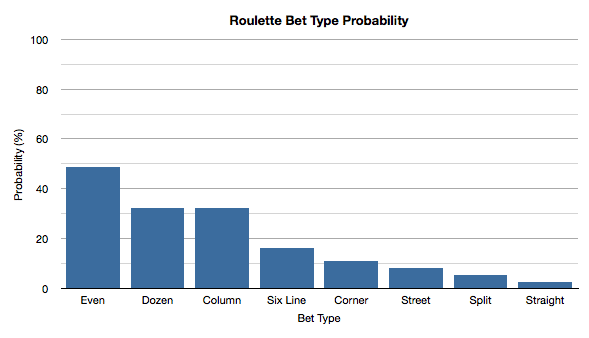
A simple bar chart to highlight the percentage probabilities of the different bet types in roulette coming in.
The same color in a row
How unlikely is it to see the same color 2 or more times in a row? What's the probability of the results of 5 spins of the roulette wheel being red? The following chart highlights the probabilities of the same color appearing over a certain number of spins of the roulette wheel.
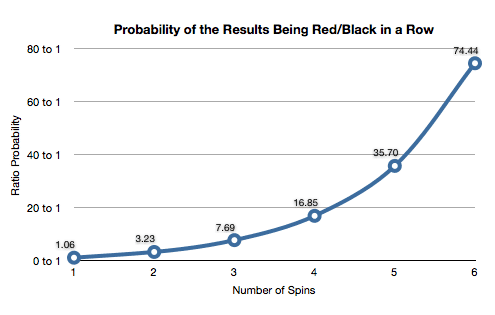
A graph to show the probability of seeing the same color of red/black (or any evens bet result for that matter) over multiple spins.
| Number of Spins | Ratio | Percentage |
|---|---|---|
| 1 | 1.06 to 1 | 48.6% |
| 2 | 3.23 to 1 | 23.7% |
| 3 | 7.69 to 1 | 11.5% |
| 4 | 16.9 to 1 | 5.60% |
| 5 | 35.7 to 1 | 2.73% |
| 6 | 74.4 to 1 | 1.33% |
| 7 | 154 to 1 | 0.65% |
| 8 | 318 to 1 | 0.31% |
| 9 | 654 to 1 | 0.15% |
| 10 | 1,346 to 1 | 0.074% |
| 15 | 49,423 to 1 | 0.0020% |
| 20 | 1,813,778 to 1 | 0.000055% |
Example: The probability of the same color showing up 4 times in a row is 5.60%.
As the graph shows, the probability of seeing the same color on consecutive spins of the roulette wheel more than halves (well, the ratio probability doubles) from one spin to the next.
I stopped the graph at 6 trials/spins, as that was enough to highlight the trend and produce a prettier probability graph.
Other probabilities
| Event | Ratio | Percentage |
|---|---|---|
| The same number (e.g. 32) over 2 spins. | 1,368 to 1 | 0.073% |
| The result being 0. | 36 to 1 | 2.7% |
| The 0 appearing at least once over 10 spins. | 2.7 to 1 | 27.0% |
| The same color over 2 spins. | 3.23 to 1 | 23.7% |
| Guessing color and even/odd correctly. | 3.11 to 1 | 24.3% |
| Guessing color and dozen correctly. | 5.16 to 1 | 16.2% |
| Guessing dozen and column correctly. | 8.25 to 1 | 10.8% |
| Rank | Casino | Rating | Payment Methods | Payout Time | Links |
|---|---|---|---|---|---|
| 1 |
|
Rating A+ | Payment Methods | Payout Time 1-2 Days | Play Now Read Review |
| 2 |
|
Rating A | Payment Methods | Payout Time 1-2 Days | Play Now Read Review |
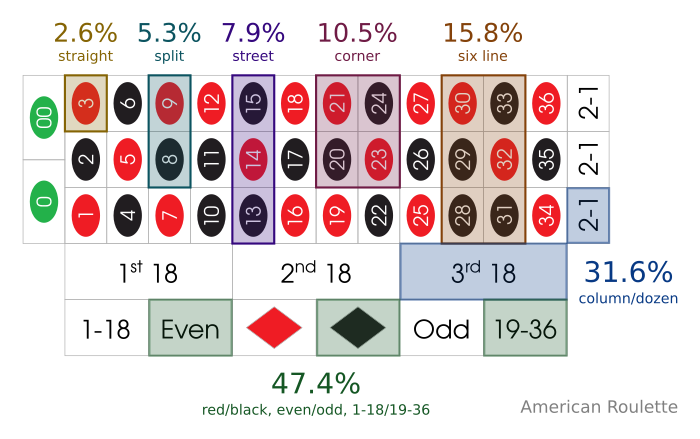
2. American roulette
Here are a few useful probabilities for American roulette.
Alongside the charts, I've included graphs that compare the American roulette probabilities to those of the European roulette probabilities. The difference in odds and probability for these two variants is explained in the American vs. European probability section below.
| Bet Type | Fraction | Ratio | Percentage |
|---|---|---|---|
| Even (e.g. Red/Black) | 1/2.11 | 1.11 to 1 | 47.4% |
| Column | 1/3.16 | 2.16 to 1 | 31.6% |
| Dozen | 1/3.16 | 2.16 to 1 | 31.6% |
| Six Line | 1/6.33 | 5.33 to 1 | 15.8% |
| Corner | 1/9.50 | 8.50 to 1 | 10.5% |
| Street | 1/12.67 | 11.67 to 1 | 7.9% |
| Split | 1/19.00 | 18.00 to 1 | 5.3% |
| Straight | 1/38.00 | 37.00 to 1 | 2.6% |
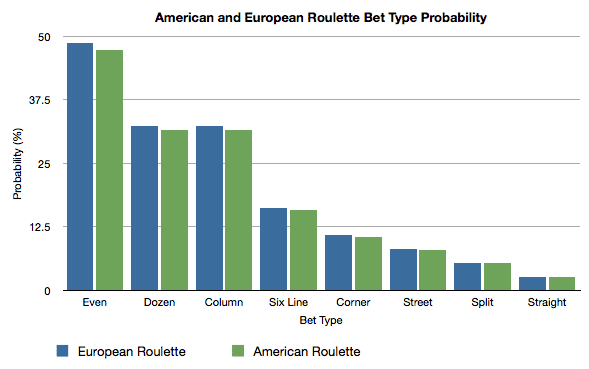
A simple bar chart to highlight the percentage probabilities of winning with the different bet types in American and European roulette.
The same color in a row
When playing on an American roulette wheel, what's the probability of seeing the same color appear X times in a row? The table below lists both the ratio and percentage probability over successive numbers of spins.
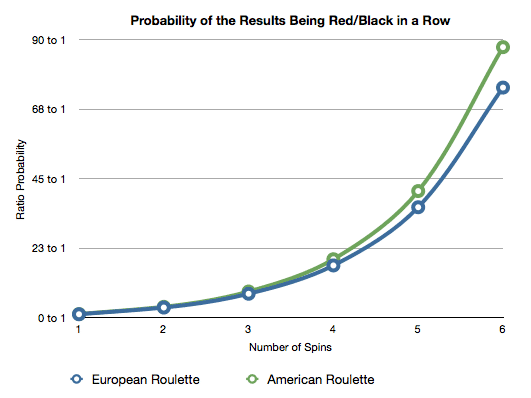
A graph to show the probability of seeing the same color of red/black on an American roulette table (compared to the odds on a European table).
| Number of Spins | Ratio | Percentage |
|---|---|---|
| 1 | 1.11 to 1 | 47.4% |
| 2 | 3.45 to 1 | 22.4% |
| 3 | 8.41 to 1 | 10.6% |
| 4 | 18.9 to 1 | 5.04% |
| 5 | 40.9 to 1 | 2.39% |
| 6 | 87.5 to 1 | 1.13% |
| 7 | 186 to 1 | 0.54% |
| 8 | 394 to 1 | 0.25% |
| 9 | 832 to 1 | 0.12% |
| 10 | 1,757 to 1 | 0.057% |
| 15 | 73,732 to 1 | 0.0014% |
| 20 | 3,091,873 to 1 | 0.000032% |
Example: The probability of the same color showing up 6 times in a row on an American roulette wheel is 1.13%.
The probability of seeing the same color appear on successive spins just over halves from one spin to the next.
You'll also notice that it's less likely to see the same color appear on multiple spins in a row on an American roulette wheel than it is on a European wheel. This is not because the American wheel is "fairer" and dishes out red/black colors more evenly — it's because there is an additional green number (the double zero - 00) that increases the likelihood of disrupting the flow of successive same-color spins.
Other probabilities
| Event | Ratio | Percentage |
|---|---|---|
| The same number (e.g. 32) over 2 spins. | 1,444 to 1 | 0.069% |
| The result being 0 or 00. | 18 to 1 | 5.26% |
| The 0 or 00 appearing at least once over 10 spins. | 0.9 to 1 | 52.6% |
| The same color over 2 spins. | 3.45 to 1 | 22.4% |
| Guessing color and even/odd correctly. | 3.22 to 1 | 23.7% |
| Guessing color and dozen correctly. | 5.33 to 1 | 15.8% |
| Guessing dozen and column correctly. | 8.5 to 1 | 10.5% |
3. Why is there a difference between European and American roulette?
The probabilities in American and European roulette are different because American roulette has an extra green number (the double zero - 00), whereas European roulette does not.
Therefore, the presence of this additional green number ever so slightly decreases the probability of hitting other specific numbers or sets of numbers, whether it be over one spin or over multiple spins.
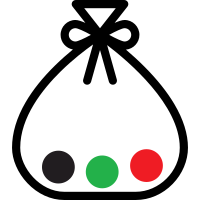
To give a simplified example, lets say I have a bag with 1 red, 1 black and 1 green ball in it. If I ask you to pick out one ball at random, the probability of choosing a red ball would be 1 in 3.
Now, if I added another green ball so that there are now 2 green balls in the bag, the probability of picking out a red ball has dropped to 1 in 4.
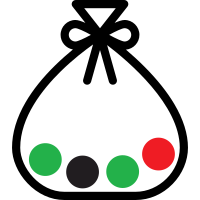
This exact same idea applies to all the probabilities in American roulette (thanks to that extra 00 number), just on a slightly bigger scale.
Fact: This difference in the probabilities also has a knock-on effect for the house edge too. So essentially, in American roulette you have a slightly worse chance of winning, but the payouts remain the same.
Note: You can find out more about the differences between these two games in my article American vs European roulette.
4. Mathematics
a. Formats
There are a number of ways to display probabilities. On the roulette charts above I have used; ratio odds, percentage odds and sometimes fractional odds. But what do they mean?
- Percentage odds (%)
- This is easy. This tells you the percentage of the time an event occurs.
- Ratio odds (X to 1)
- For every time X happens, the event will occur 1 time.
Example: The ratio odds of a specific number appearing are 36 to 1, which means that for every 36 times the number doesn't appear, it will appear 1 time. - Fractional odds (1/X)
- The event occurs 1 time out of X amount of trials.
Example: The fractional odds of a specific number appearing are 1/37, which means that it will happen 1 time out of 37 spins.
As you can see, fractional odds and ratio odds are pretty similar. The main difference is that fractional odds uses the total number of spins, whereas the ratio just splits it up in to two parts.
The majority of people are most comfortable using percentage odds, as they're the most widely understood. Feel free to use whatever makes the most sense to you though of course. They all point to the same thing at the end of the day.
b. Calculating
From my experience, the easiest way to work out probabilities in roulette is to look at the fraction of numbers for your desired probability, then convert to a percentage or ratio from there.
For example, lets say you want to know the probability of the result being red on a European wheel. Well, there are 18 red numbers and 37 numbers in total, so the fractional probability is 18/37. Simple.
With this easy-to-get fractional probability, you can then convert it to a ratio or percentage.
Single spin
Calculation: Count the amount of numbers that give you the result you want to find the probability for, then put that number over 37 (the total number of possible results).
For example, the probability of:
- Red = 18/37 (there are 18 red numbers)
- Even = 18/37 (there are 18 even numbers)
- Dozen = 12/37 (there are 12 numbers in a dozen bet)
- 8 Black = 1/37 (there is only one number 8)
- Red and Odd = 9/37 (there are 9 numbers that are both red and odd)
- Dozen and Column = 4/37 (there are only 4 numbers in the same dozen and column)
As well as working out the probability of winning on each spin, you can also find the likelihood of losing on each spin. All you have to do is count the numbers that will result in a loss. For example, the probability of losing if you bet on red is 19/37 (18 black numbers + 1 green number).
Note: To reduce a fraction down to 1/X, just divide each side by the number on the left. e.g. a bet on red has the probability of 18/37, divide each side by 18 and you've got 1/2.05.
Multiple spins
Calculation: Work out the fractional probability for each individual spin (as above), then multiply those fractions together.
For example, let's say you want to find the probability of making correct guesses on specific bet types over multiple spins:
- Spin 1: Red = 18/37
- Spin 2: Dozen bet = 12/37
- Probability = (18/37) x (12/37) = 1/6.34
- Spin 1: Straight Bet (e.g. 32) = 1/37
- Spin 2: Straight Bet (e.g. 15) = 1/37
- Probability = (1/37) x (1/37) = 1/1369
- Spin 1: Black and Even = 9/37
- Spin 2: Odd = 18/37
- Spin 3: Column = 12/37
- Probability = (9/37) x (18/37) x (12/37) = 1/26.06
To keep it simple, I reduced the all fractions for the results above down to the 1/X format.
c. Converting
Having probabilities in a fraction format like 18/37 or 1/2.05 is okay, but sometimes it's more useful to see the probability as a percentage or a ratio. Luckily, it's pretty easy to convert to either of these from a fraction.
Fraction to ratio
Conversion: Reduce the fraction to the 1/X format, then take 1 away from X. This will give you the X to 1 ratio.
For example, what is a dozen bet (12/37) as a ratio?
- Reduce the fraction to 1/X. 12/37 = 1/3.08 (you divide both sides by the left-hand side number, which in this example is 12)
- Take 1 away from X. 3.08 - 1 = 2.08
- Ratio = 2.08 to 1
Fraction to percentage
Conversion: Divide the left side by the right side, then multiply by 100.
For example, what is a corner bet (4/37) as a percentage?
- Divide the left side by the right side. 4 ÷ 37 = 0.1081
- Multiply by 100. 0.1081 x 100 = 10.81%
- Percentage = 10.81%
5. Important fact about probability
The result of the next spin is never influenced by the result of previous spins.
A quick example
The probability of the result being red on one spin of the wheel is 48.6%. That's easy enough.
Now, what if I told you that over the last 10 spins, the result had been black each time. What do you think the probability of the result being red on the next spin would be? Higher than 48.6%?
Wrong. The probability would be exactly 48.6% again.
Why?
The roulette wheel doesn't think "I've only delivered black results over the last 10 spins, I better increase the probability of the next result being red to even things up". Unfortunately, roulette wheels are not that thoughtful.
If you had just sat down at the roulette table and didn't know that the last 10 spins were black, you wouldn't have a hard time agreeing that the probability of seeing a red on the next spin is 48.6%. Yet if you are aware of recent results, you're tempted to let it affect your judgment.
Each and every result is independent of the last, so don't expect the results of future spins to be affected by the results you've seen over previous spins. If you can learn to appreciate this fact, you will save yourself from some disappointment (and frustration) in the future.
Believing that a certain result is "due" because of past results is known as the gambler's fallacy.
What about those graphs above?
In the graph of the probability of seeing the same color over multiple spins of the wheel, it shows that the probability of the result being the same color halves from one spin to the next.
However, this is only if you're looking at the entire set of trials/spins from the start.
If the last spin was red, the chances of the next spin being red are still 48.6% — they do not drop to 23.7%. On the other hand, if you hadn't spun the wheel to see the first red result and wanted to know the probability of seeing red over the next 2 spins (and not just on the next 1 spin), the probability would be 23.7%.
Further reading
- Roulette Winnings Simulator
- American Roulette House Edge - wizardofodds.com
- Gambling Expectation - hundredpercentgambling.com